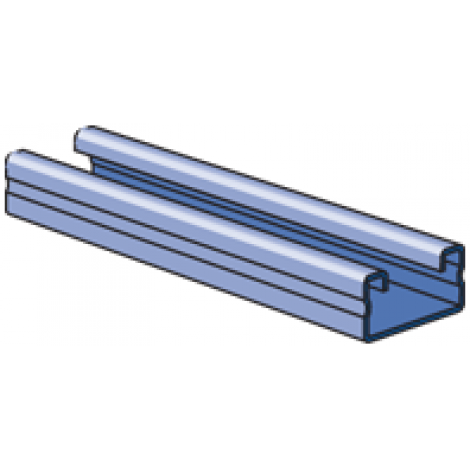
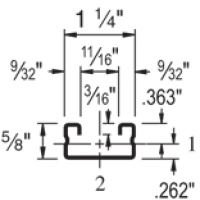
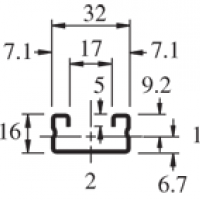
| Elements of Section - A4000 | ||
| Area of Section | 0.132 in2 (0.9 cm2) | |
Axis 1-1 | Axis 2-2 | |
| Moment of Inertia (I) | 0.008 in4 (0.3 cm4) | 0.029 in4 (1.2 cm4) |
| Section Modulus (S) | 0.022 in3 (0.4 cm3) | 0.046 in3 (0.8 cm3) |
| Radius of Gyration (r) | 0.240 in (0.6 cm ) | 0.469 in (1.2 cm ) |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beam Loading - A4000 | ||||||
| Span (in) | Max Allowable Uniform | Defl at Uniform load (in) | Uniform Loading at Deflection | Lateral Bracing Reduction Factor | ||
| Span /180 (lbs) | Span /240 | Span /360 (lbs) | ||||
| 18 | 250 | 0.08 | 250 | 220 | 150 | 1.00 |
| 24 | 190 | 0.15 | 170 | 120 | 80 | 0.94 |
| 36 | 120 | 0.32 | 70 | 60 | 40 | 0.83 |
| 48 | 90 | 0.58 | 40 | 30 | 20 | 0.73 |
| 60 | 70 | 0.88 | 30 | 20 | 10 | 0.65 |
| 72 | 60 | 1.30 | 20 | 10 | 10 | 0.58 |
Notes:
- Above loads include the weight of the member. This weight must be deducted to arrive at the net allowable load the beam will support.
- Long span beams should be supported so as to prevent rotation and twist.
- Allowable uniformly distributed loads are listed for various simple spans, that is, a beam on two supports. If load is concentrated at the center of the span, multiply load from the table by 0.5 and corresponding deflection by 0.8.
- The lateral bracing factor should be multiplied by the load to determine the load retained based on the distance between lateral braces.
Bearing Load on Channel:
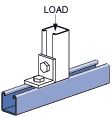 | 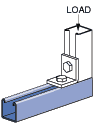 |
| Max Load 1,400 Lbs635 Kg | Max Load 1,000 Lbs454 Kg |